Choice Models

import larch as lx

In this guide, we’ll take a look at building a discrete choice model using Larch. We assume you have a decent grasp of the fundamentals of choice modeling – if not, we suggest reading the Discrete Choice Modeling section of the Python for Transportation Modeling course.

Some addition advanced or detailed topics are broken out into seperate guides:

• Data Fundamentals for Choice Models

• Working with Linear Functions

• Machine Learning Integration

The examples below work with the tiny dataset introduced in the Data Fundamentals section.

Show code cell content

Hide code cell content

# HIDDEN
df_ca = pd.read_csv("example-data/tiny_idca.csv")
cats = df_ca["altid"].astype(pd.CategoricalDtype(["Car", "Bus", "Walk"])).cat
df_ca["altnum"] = cats.codes + 1
df_ca = df_ca.set_index(["caseid", "altnum"])
data = lx.Dataset.construct.from_idca(df_ca.sort_index(), fill_missing=0)
data = data.drop_vars("_avail_")
data["ChosenCode"] = (data["Chosen"] * data["Chosen"].altnum).sum("altnum")
data.coords["alt_names"] = lx.DataArray(
    cats.categories, dims=("altnum"), coords={"altnum": data.altnum}
)
alts = dict(zip(data["altnum"].values, data["alt_names"].values))
for i, k in alts.items():
    data[f"{k}Time"] = data["Time"].sel(altnum=i)

/opt/hostedtoolcache/Python/3.10.18/x64/lib/python3.10/site-packages/xarray/core/duck_array_ops.py:253: RuntimeWarning: invalid value encountered in cast
  return data.astype(dtype, **kwargs)

data

<xarray.Dataset> Size: 603B
Dimensions:     (caseid: 4, altnum: 3)
Coordinates:
  * caseid      (caseid) int64 32B 1 2 3 4
  * altnum      (altnum) int8 3B 1 2 3
    alt_names   (altnum) object 24B 'Car' 'Bus' 'Walk'
Data variables:
    altid       (caseid, altnum) object 96B 'Car' 'Bus' 'Walk' ... 'Bus' 'Walk'
    Income      (caseid) int64 32B 30000 30000 40000 50000
    Time        (caseid, altnum) int64 96B 30 40 20 25 35 0 40 50 30 15 20 10
    Cost        (caseid, altnum) int64 96B 150 100 0 125 100 ... 75 0 225 150 0
    Chosen      (caseid, altnum) int64 96B 1 0 0 0 1 0 0 0 1 0 0 1
    ChosenCode  (caseid) int64 32B 1 2 3 3
    CarTime     (caseid) int64 32B 30 25 40 15
    BusTime     (caseid) int64 32B 40 35 50 20
    WalkTime    (caseid) int64 32B 20 0 30 10
Attributes:
    _caseid_:  caseid
    _altid_:   altnum

xarray.Dataset

• Dimensions:
  • caseid: 4
  • altnum: 3
• Coordinates: (3)
  • caseid
    (caseid)
    int64
    1 2 3 4

    array([1, 2, 3, 4])

  • altnum
    (altnum)
    int8
    1 2 3

    array([1, 2, 3], dtype=int8)

  • alt_names
    (altnum)
    object
    'Car' 'Bus' 'Walk'

    array(['Car', 'Bus', 'Walk'], dtype=object)

• Data variables: (9)
  • altid
    (caseid, altnum)
    object
    'Car' 'Bus' 'Walk' ... 'Bus' 'Walk'

    array([['Car', 'Bus', 'Walk'],
           ['Car', 'Bus', 0],
           ['Car', 'Bus', 'Walk'],
           ['Car', 'Bus', 'Walk']], dtype=object)

  • Income
    (caseid)
    int64
    30000 30000 40000 50000

    array([30000, 30000, 40000, 50000])

  • Time
    (caseid, altnum)
    int64
    30 40 20 25 35 0 40 50 30 15 20 10

    array([[30, 40, 20],
           [25, 35,  0],
           [40, 50, 30],
           [15, 20, 10]])

  • Cost
    (caseid, altnum)
    int64
    150 100 0 125 100 ... 0 225 150 0

    array([[150, 100,   0],
           [125, 100,   0],
           [125,  75,   0],
           [225, 150,   0]])

  • Chosen
    (caseid, altnum)
    int64
    1 0 0 0 1 0 0 0 1 0 0 1

    array([[1, 0, 0],
           [0, 1, 0],
           [0, 0, 1],
           [0, 0, 1]])

  • ChosenCode
    (caseid)
    int64
    1 2 3 3

    array([1, 2, 3, 3])

  • CarTime
    (caseid)
    int64
    30 25 40 15

    array([30, 25, 40, 15])

  • BusTime
    (caseid)
    int64
    40 35 50 20

    array([40, 35, 50, 20])

  • WalkTime
    (caseid)
    int64
    20 0 30 10

    array([20,  0, 30, 10])

• Indexes: (2)
  • caseid
    PandasIndex

    PandasIndex(Index([1, 2, 3, 4], dtype='int64', name='caseid'))

  • altnum
    PandasIndex

    PandasIndex(Index([1, 2, 3], dtype='int8', name='altnum'))

• Attributes: (2)

  _caseid_ :

  caseid

  _altid_ :

  altnum

The basic structure of a choice model in Larch is contained in the Model object.

m = lx.Model(data)

Alternatives

The universe of possible alternatives is generally defined by the data object, not in the model itself. If the data is defined simply by a Dataset, the _altid_ attribute of that dataset indicates the name of the dimension that represents the alternatives.

data.attrs["_altid_"]

'altnum'

For convenience, Larch adds a dc accessor to Datasets, to manipulate the discrete choice facets of the data. This allows access to the alternative codes (the coordinate vector for the alts dimension) via the altids method, and a dictionary mapping codes to names in the alts_mapping property.

data.dc.altids()

Index([1, 2, 3], dtype='int8', name='altnum')

data.dc.alts_mapping

{np.int8(1): 'Car', np.int8(2): 'Bus', np.int8(3): 'Walk'}

If you have a dataset that is missing alternative codes, or if you want to replace the existing alternative codes, you can use the set_altids method.

data.dc.set_altids([1, 2, 3, 4], dim_name="newalts")

<xarray.Dataset> Size: 635B
Dimensions:     (caseid: 4, altnum: 3, newalts: 4)
Coordinates:
  * caseid      (caseid) int64 32B 1 2 3 4
  * altnum      (altnum) int8 3B 1 2 3
    alt_names   (altnum) object 24B 'Car' 'Bus' 'Walk'
  * newalts     (newalts) int64 32B 1 2 3 4
Data variables:
    altid       (caseid, altnum) object 96B 'Car' 'Bus' 'Walk' ... 'Bus' 'Walk'
    Income      (caseid) int64 32B 30000 30000 40000 50000
    Time        (caseid, altnum) int64 96B 30 40 20 25 35 0 40 50 30 15 20 10
    Cost        (caseid, altnum) int64 96B 150 100 0 125 100 ... 75 0 225 150 0
    Chosen      (caseid, altnum) int64 96B 1 0 0 0 1 0 0 0 1 0 0 1
    ChosenCode  (caseid) int64 32B 1 2 3 3
    CarTime     (caseid) int64 32B 30 25 40 15
    BusTime     (caseid) int64 32B 40 35 50 20
    WalkTime    (caseid) int64 32B 20 0 30 10
Attributes:
    _caseid_:  caseid
    _altid_:   newalts

xarray.Dataset

• Dimensions:
  • caseid: 4
  • altnum: 3
  • newalts: 4
• Coordinates: (4)
  • caseid
    (caseid)
    int64
    1 2 3 4

    array([1, 2, 3, 4])

  • altnum
    (altnum)
    int8
    1 2 3

    array([1, 2, 3], dtype=int8)

  • alt_names
    (altnum)
    object
    'Car' 'Bus' 'Walk'

    array(['Car', 'Bus', 'Walk'], dtype=object)

  • newalts
    (newalts)
    int64
    1 2 3 4

    array([1, 2, 3, 4])

• Data variables: (9)
  • altid
    (caseid, altnum)
    object
    'Car' 'Bus' 'Walk' ... 'Bus' 'Walk'

    array([['Car', 'Bus', 'Walk'],
           ['Car', 'Bus', 0],
           ['Car', 'Bus', 'Walk'],
           ['Car', 'Bus', 'Walk']], dtype=object)

  • Income
    (caseid)
    int64
    30000 30000 40000 50000

    array([30000, 30000, 40000, 50000])

  • Time
    (caseid, altnum)
    int64
    30 40 20 25 35 0 40 50 30 15 20 10

    array([[30, 40, 20],
           [25, 35,  0],
           [40, 50, 30],
           [15, 20, 10]])

  • Cost
    (caseid, altnum)
    int64
    150 100 0 125 100 ... 0 225 150 0

    array([[150, 100,   0],
           [125, 100,   0],
           [125,  75,   0],
           [225, 150,   0]])

  • Chosen
    (caseid, altnum)
    int64
    1 0 0 0 1 0 0 0 1 0 0 1

    array([[1, 0, 0],
           [0, 1, 0],
           [0, 0, 1],
           [0, 0, 1]])

  • ChosenCode
    (caseid)
    int64
    1 2 3 3

    array([1, 2, 3, 3])

  • CarTime
    (caseid)
    int64
    30 25 40 15

    array([30, 25, 40, 15])

  • BusTime
    (caseid)
    int64
    40 35 50 20

    array([40, 35, 50, 20])

  • WalkTime
    (caseid)
    int64
    20 0 30 10

    array([20,  0, 30, 10])

• Indexes: (3)
  • caseid
    PandasIndex

    PandasIndex(Index([1, 2, 3, 4], dtype='int64', name='caseid'))

  • altnum
    PandasIndex

    PandasIndex(Index([1, 2, 3], dtype='int8', name='altnum'))

  • newalts
    PandasIndex

    PandasIndex(Index([1, 2, 3, 4], dtype='int64', name='newalts'))

• Attributes: (2)

  _caseid_ :

  caseid

  _altid_ :

  newalts

Choices

The dependent variable for a discrete choice model is an array that describes the choices. In Larch, there are three different ways to indicate choices, by assigning to different attributes:

m.choice_ca_var : The choices are given by indicator values (typically but not neccessarily dummy variables) in an idca variable.

m.choice_co_code : The choices are given by altid values in an idco variable. These choice codes are then converted to binary indicators by Larch.

m.choice_co_vars : The choices are given by indicator values (typically but not neccessarily dummy variables) in multiple idco variables, one for each alternative.

Given the dataset (which has all these formats defined), all the following choice definitions result in the same choice representation:

m.choice_co_code = "ChosenCode"

m.choice_co_vars = {
    1: "ChosenCode == 1",
    2: "ChosenCode == 2",
    3: "ChosenCode == 3",
}

m.choice_ca_var = "Chosen"

After setting the choice definition, the loaded or computed choice array should be available as the 'ch' DataArray in the model’s dataset.

m.dataset["ch"]

<xarray.DataArray 'ch' (caseid: 4, altnum: 3)> Size: 96B
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.],
       [0., 0., 1.]])
Coordinates:
  * caseid     (caseid) int64 32B 1 2 3 4
  * altnum     (altnum) int8 3B 1 2 3
    alt_names  (altnum) object 24B 'Car' 'Bus' 'Walk'

xarray.DataArray

'ch'

• caseid: 4
• altnum: 3

• 1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0 0.0 0.0 1.0

  array([[1., 0., 0.],
         [0., 1., 0.],
         [0., 0., 1.],
         [0., 0., 1.]])

• Coordinates: (3)
  • caseid
    (caseid)
    int64
    1 2 3 4

    array([1, 2, 3, 4])

  • altnum
    (altnum)
    int8
    1 2 3

    array([1, 2, 3], dtype=int8)

  • alt_names
    (altnum)
    object
    'Car' 'Bus' 'Walk'

    array(['Car', 'Bus', 'Walk'], dtype=object)

• Indexes: (2)
  • caseid
    PandasIndex

    PandasIndex(Index([1, 2, 3, 4], dtype='int64', name='caseid'))

  • altnum
    PandasIndex

    PandasIndex(Index([1, 2, 3], dtype='int8', name='altnum'))

• Attributes: (0)

Availability

In addition to the choices, we can also define an array that describes the availability of the various alternatives. Unlike the choices, for the availability factors we expect that we’ll need to toggle the availability on or off for potentially every alternative in each case, so there’s only two ways to define availability, by assigning to attributes:

m.availability_ca_var : The availability of alternatives is given by binary values (booleans, or equivalent integers) in an idca variable.

m.availability_co_vars : The availability of alternatives is given by binary values (booleans, or equivalent integers) in multiple idco variables, one for each alternative.

Given the dataset, both of the following availability definitions result in the same availability representation:

m.availability_ca_var = "Time > 0"

m.availability_co_vars = {
    1: True,
    2: "BusTime > 0",
    3: "WalkTime > 0",
}

After setting the availability definition, the loaded or computed availability array should be available as the 'av' DataArray in the model’s dataset.

m.dataset["av"]

<xarray.DataArray 'av' (caseid: 4, altnum: 3)> Size: 96B
array([[1, 1, 1],
       [1, 1, 0],
       [1, 1, 1],
       [1, 1, 1]])
Coordinates:
  * caseid     (caseid) int64 32B 1 2 3 4
  * altnum     (altnum) int8 3B 1 2 3
    alt_names  (altnum) object 24B 'Car' 'Bus' 'Walk'

xarray.DataArray

'av'

• caseid: 4
• altnum: 3

• 1 1 1 1 1 0 1 1 1 1 1 1

  array([[1, 1, 1],
         [1, 1, 0],
         [1, 1, 1],
         [1, 1, 1]])

• Coordinates: (3)
  • caseid
    (caseid)
    int64
    1 2 3 4

    array([1, 2, 3, 4])

  • altnum
    (altnum)
    int8
    1 2 3

    array([1, 2, 3], dtype=int8)

  • alt_names
    (altnum)
    object
    'Car' 'Bus' 'Walk'

    array(['Car', 'Bus', 'Walk'], dtype=object)

• Indexes: (2)
  • caseid
    PandasIndex

    PandasIndex(Index([1, 2, 3, 4], dtype='int64', name='caseid'))

  • altnum
    PandasIndex

    PandasIndex(Index([1, 2, 3], dtype='int8', name='altnum'))

• Attributes: (0)

Utility Functions

Choice models in Larch rely on utility expressions that are linear-in-parameters functions, which combine parameters P and data X. You can attach these function expressions to the model in two ways:

m.utility_ca : A linear function containing generic expressions that are evaluated against the idca portion of the dataset. These expression can technically also reference idco variables, but to define a well-specified choice model with identifiable parameters, each data term will need at least one idca component.

m.utility_co : A mapping of alternative-specific expressions that are evaluated against only the idco portion of the dataset. Each key gives an alternative id, and the values are linear functions.

These two utility function definitions are not mutually exclusive, and you can mix both types of functions in the same model.

from larch import P, X

m.utility_ca = P.Time * X.Time + P.Cost * X.Cost

m.utility_co = {
    1: P.Income_Car * X.Income / 1000,
    2: P.Income_Bus * X.Income / 1000,
}

The computed values for the utility function can be accessed using the utility method, which also permits the user to set new values for various model parameters.

m.utility(
    {"Time": -0.01, "Cost": -0.02, "Income_Car": 0.1},
    return_format="dataarray",
)

<xarray.DataArray (caseid: 4, nodeid: 4)> Size: 128B
array([[-0.3       , -2.4       , -0.2       ,  0.50093705],
       [ 0.25      , -2.35      ,        -inf,  0.32164469],
       [ 1.1       , -2.        , -0.3       ,  1.3559175 ],
       [ 0.35      , -3.2       , -0.1       ,  0.86063728]])
Coordinates:
  * caseid     (caseid) int64 32B 1 2 3 4
  * nodeid     (nodeid) int64 32B 1 2 3 0
    node_name  (nodeid) <U6 96B 'Car' 'Bus' 'Walk' '_root_'

xarray.DataArray

• caseid: 4
• nodeid: 4

• -0.3 -2.4 -0.2 0.5009 0.25 -2.35 ... -0.3 1.356 0.35 -3.2 -0.1 0.8606

  array([[-0.3       , -2.4       , -0.2       ,  0.50093705],
         [ 0.25      , -2.35      ,        -inf,  0.32164469],
         [ 1.1       , -2.        , -0.3       ,  1.3559175 ],
         [ 0.35      , -3.2       , -0.1       ,  0.86063728]])

• Coordinates: (3)
  • caseid
    (caseid)
    int64
    1 2 3 4

    array([1, 2, 3, 4])

  • nodeid
    (nodeid)
    int64
    1 2 3 0

    array([1, 2, 3, 0])

  • node_name
    (nodeid)
    <U6
    'Car' 'Bus' 'Walk' '_root_'

    array(['Car', 'Bus', 'Walk', '_root_'], dtype='<U6')

• Indexes: (2)
  • caseid
    PandasIndex

    PandasIndex(Index([1, 2, 3, 4], dtype='int64', name='caseid'))

  • nodeid
    PandasIndex

    PandasIndex(Index([1, 2, 3, 0], dtype='int64', name='nodeid'))

• Attributes: (0)

Data Preparation

Larch works with two “tiers” of data:

m.datatree : A DataTree that holds the raw data used for the model. This can consist of just a single Dataset, (which is automatically converted into a one-node tree when you assign it to this attribute) or multiple related datasets linked together using the sharrow library.

m.dataset : The assembled arrays actually used in calculation, stored as a Dataset that has variables for various required data elements and dimensions structured to support the model design. The dataset is wiped out when any aspect of the model structure is changed, and rebuilt as needed for computation. For particular applications that require specialized optimization, the dataset can be provided exogenously after the model stucture is finalized, but generally it will be convenient for users to let Larch build the dataset automatically from a datatree.

m.datatree

<larch.dataset.DataTree>
 datasets:
 - main
 relationships: none

m.dataset

<xarray.Dataset> Size: 531B
Dimensions:    (caseid: 4, altnum: 3, var_co: 1, var_ca: 2)
Coordinates:
  * caseid     (caseid) int64 32B 1 2 3 4
  * altnum     (altnum) int8 3B 1 2 3
    alt_names  (altnum) object 24B 'Car' 'Bus' 'Walk'
  * var_co     (var_co) <U6 24B 'Income'
  * var_ca     (var_ca) <U4 32B 'Cost' 'Time'
Data variables:
    co         (caseid, var_co) float64 32B 3e+04 3e+04 4e+04 5e+04
    ca         (caseid, altnum, var_ca) float64 192B 150.0 30.0 ... 0.0 10.0
    ch         (caseid, altnum) float64 96B 1.0 0.0 0.0 0.0 ... 1.0 0.0 0.0 1.0
    av         (caseid, altnum) int64 96B 1 1 1 1 1 0 1 1 1 1 1 1
Attributes:
    _caseid_:  caseid
    _altid_:   altnum

xarray.Dataset

• Dimensions:
  • caseid: 4
  • altnum: 3
  • var_co: 1
  • var_ca: 2
• Coordinates: (5)
  • caseid
    (caseid)
    int64
    1 2 3 4

    array([1, 2, 3, 4])

  • altnum
    (altnum)
    int8
    1 2 3

    array([1, 2, 3], dtype=int8)

  • alt_names
    (altnum)
    object
    'Car' 'Bus' 'Walk'

    array(['Car', 'Bus', 'Walk'], dtype=object)

  • var_co
    (var_co)
    <U6
    'Income'

    array(['Income'], dtype='<U6')

  • var_ca
    (var_ca)
    <U4
    'Cost' 'Time'

    array(['Cost', 'Time'], dtype='<U4')

• Data variables: (4)
  • co
    (caseid, var_co)
    float64
    3e+04 3e+04 4e+04 5e+04

    array([[30000.],
           [30000.],
           [40000.],
           [50000.]])

  • ca
    (caseid, altnum, var_ca)
    float64
    150.0 30.0 100.0 ... 20.0 0.0 10.0

    array([[[150.,  30.],
            [100.,  40.],
            [  0.,  20.]],
    
           [[125.,  25.],
            [100.,  35.],
            [  0.,   0.]],
    
           [[125.,  40.],
            [ 75.,  50.],
            [  0.,  30.]],
    
           [[225.,  15.],
            [150.,  20.],
            [  0.,  10.]]])

  • ch
    (caseid, altnum)
    float64
    1.0 0.0 0.0 0.0 ... 1.0 0.0 0.0 1.0

    array([[1., 0., 0.],
           [0., 1., 0.],
           [0., 0., 1.],
           [0., 0., 1.]])

  • av
    (caseid, altnum)
    int64
    1 1 1 1 1 0 1 1 1 1 1 1

    array([[1, 1, 1],
           [1, 1, 0],
           [1, 1, 1],
           [1, 1, 1]])

• Indexes: (4)
  • caseid
    PandasIndex

    PandasIndex(Index([1, 2, 3, 4], dtype='int64', name='caseid'))

  • altnum
    PandasIndex

    PandasIndex(Index([1, 2, 3], dtype='int8', name='altnum'))

  • var_co
    PandasIndex

    PandasIndex(Index(['Income'], dtype='object', name='var_co'))

  • var_ca
    PandasIndex

    PandasIndex(Index(['Cost', 'Time'], dtype='object', name='var_ca'))

• Attributes: (2)

  _caseid_ :

  caseid

  _altid_ :

  altnum

Nesting Structures

By default, a model in Larch is assumed to be a simple multinomial logit model, unless a nesting structure is defined. That structure is defined in a model’s graph.

m.graph

Adding a nest can be accomplished the the new_node method, which allows you to give a nesting node’s child codes, a name, and attach a logsum parameter.

z = m.graph.new_node(parameter="Mu_Motorized", children=[1, 2], name="Motorized")
m.graph

The return value of new_node is the code number of the new nest. This is assigned automatically so as to not overlap with any other alternatives or nests. We can use this to develop multi-level nesting structures, by putting that new code number as the child for yet another new nest.

m.graph.new_node(parameter="Mu_Omni", children=[z, 3], name="Omni")
m.graph

Nothing in Larch prevents you from overloading the nesting structure with degenerate nests, as shown above. You may have difficult with estimating parameters if you are not careful with such complex structures. If you need to remove_node, you can do so by giving its code–but you’ll likely find you’ll be much better off just fixing your code and starting over, as node removal can have some odd side effects for complex structures.

m.graph.remove_node(5)
m.graph

Parameter Estimation

Larch can automatically find all the model parameters contained in the model specification, so we don’t need to address them separately unless we want to modify any defaults.

We can review the parameters Larch has found, as well as the current values set for them, in the parameter frame, or pf.

m.pf

	value	best	initvalue	minimum	maximum	nullvalue	holdfast
param_name
Cost	-0.02	-0.02	0.0	-inf	inf	0.0	0
Income_Bus	0.00	NaN	0.0	-inf	inf	0.0	0
Income_Car	0.10	NaN	0.0	-inf	inf	0.0	0
Mu_Motorized	1.00	NaN	1.0	0.01	1.0	1.0	0
Time	-0.01	-0.01	0.0	-inf	inf	0.0	0

If we want to set certain parameters to be constrained to be certain values, that can be accomplished with the plock method. Because our sample data has so few observations, it won’t be possible to estimate values for all four parameters, so we can assert values for two of them.

m.plock({"Time": -0.01, "Cost": -0.02})
m.pf

	value	best	initvalue	minimum	maximum	nullvalue	holdfast
param_name
Cost	-0.02	-0.02	-0.02	-inf	inf	0.0	1
Income_Bus	0.00	NaN	0.00	-inf	inf	0.0	0
Income_Car	0.10	NaN	0.00	-inf	inf	0.0	0
Mu_Motorized	1.00	NaN	1.00	0.01	1.0	1.0	0
Time	-0.01	-0.01	-0.01	-inf	inf	0.0	1

The default infinite bounds on the remaining parameters can be problematic for some optimization algorithms, so it’s usually good practice to set large but finite limits for those values. The set_cap method can do just that, setting a minimum and maximum value for all the parameters that otherwise have bounds outside the cap.

m.set_cap(100)
m.pf

	value	best	initvalue	minimum	maximum	nullvalue	holdfast
param_name
Cost	-0.02	-0.02	-0.02	-inf	inf	0.0	1
Income_Bus	0.00	NaN	0.00	-100.00	100.0	0.0	0
Income_Car	0.10	NaN	0.00	-100.00	100.0	0.0	0
Mu_Motorized	1.00	NaN	1.00	0.01	1.0	1.0	0
Time	-0.01	-0.01	-0.01	-inf	inf	0.0	1

To actually develop maximum likelihood estimates for the remaining unconstrained parameters, use the maximize_loglike method.

m.maximize_loglike()

Iteration 007 [Optimization terminated successfully]

Best LL = -3.8172546401484566

	value	best	initvalue	minimum	maximum	nullvalue	holdfast
param_name
Cost	-0.020000	-0.020000	-0.02	-inf	inf	0.0	1
Income_Bus	0.028418	0.028418	0.00	-100.00	100.0	0.0	0
Income_Car	0.047842	0.047842	0.00	-100.00	100.0	0.0	0
Mu_Motorized	1.000000	1.000000	1.00	0.01	1.0	1.0	0
Time	-0.010000	-0.010000	-0.01	-inf	inf	0.0	1

key	value
x	0 Cost -0.020000 Income_Bus 0.028418 Income_Car 0.047842 Mu_Motorized 1.000000 Time -0.010000
logloss	np.float64(0.9543136600371142)
d_logloss	0 Cost 0.000000 Income_Bus -0.000264 Income_Car 0.000208 Mu_Motorized 0.098815 Time 0.000000
nit	7
nfev	13
njev	7
status	0
message	'Optimization terminated successfully'
success	np.True_
elapsed_time	0:00:00.064715
method	'slsqp'
n_cases	4
iteration_number	7
loglike	np.float64(-3.8172546401484566)

In a Jupyter notebook, this method displays a live-updating view of the progress of the optmization algorithm, so that the analyst can interrupt if something looks wrong.

The maximize_loglike method does not include the calculation of parameter covariance matrixes, standard errors, or t-statistics. For large models, this can be a computationally expensive process, and it is often but not always necessary. Those computatations are made in the calculate_parameter_covariance method instead. Once completed, things like t-statistics and standard errors are available in the parameter frame.

m.calculate_parameter_covariance()
m.pf

	value	best	initvalue	minimum	maximum	nullvalue	holdfast
param_name
Cost	-0.020000	-0.020000	-0.02	-inf	inf	0.0	1
Income_Bus	0.028418	0.028418	0.00	-100.00	100.0	0.0	0
Income_Car	0.047842	0.047842	0.00	-100.00	100.0	0.0	0
Mu_Motorized	1.000000	1.000000	1.00	0.01	1.0	1.0	0
Time	-0.010000	-0.010000	-0.01	-inf	inf	0.0	1

Overspecification

Overspecification in a discrete choice model occurs when the model includes more explanatory variables (independent variables) than necessary or relevant for accurately predicting choice behaviors. A particular computational flavor of overspecification is multicollinearity, which is when independent variables are highly (or perfectly) correlated with each other. This makes it difficult to estimate the true effect of each variable on the dependent variable (choice behavior) and can lead to unstable parameter estimates. To demonstrate this, we can create a copy of the model and add an Income_Walk term to the utility function.

m2 = m.copy()
m2.utility_co[3] = P.Income_Walk * X.Income / 1000

The three Income_* terms now in the model now form a closed loop, such that the sum of all three of these terms is always 1. The result is an overspecified model. Larch doesn’t stop you from doing this, and may even estimate parameters successfully with the maximize_loglike function.

m2.maximize_loglike()

Iteration 001 [Optimization terminated successfully]

Best LL = -3.8172546356353823

	value	best	initvalue	minimum	maximum	nullvalue	holdfast
param_name
Cost	-0.020000	-0.020000	-0.02	-inf	inf	0.0	1
Income_Bus	0.028418	0.028418	0.00	-100.00	100.0	0.0	0
Income_Car	0.047842	0.047842	0.00	-100.00	100.0	0.0	0
Income_Walk	0.000000	0.000000	0.00	-inf	inf	0.0	0
Mu_Motorized	1.000000	1.000000	1.00	0.01	1.0	1.0	0
Time	-0.010000	-0.010000	-0.01	-inf	inf	0.0	1

/opt/hostedtoolcache/Python/3.10.18/x64/lib/python3.10/site-packages/larch/model/optimization.py:338: UserWarning: slsqp may not play nicely with unbounded parameters
if you get poor results, consider setting global bounds with model.set_cap()
  warnings.warn(  # infinite bounds #  )

key	value
x	0 Cost -0.020000 Income_Bus 0.028418 Income_Car 0.047842 Income_Walk 0.000000 Mu_Motorized 1.000000 Time -0.010000
logloss	np.float64(0.9543136589088456)
d_logloss	0 Cost 0.000000 Income_Bus -0.000264 Income_Car 0.000208 Income_Walk 0.000056 Mu_Motorized 0.098815 Time 0.000000
nit	1
nfev	1
njev	1
status	0
message	'Optimization terminated successfully'
success	np.True_
elapsed_time	0:00:00.022103
method	'slsqp'
n_cases	4
iteration_number	1
loglike	np.float64(-3.8172546356353823)

However, when you attempt to calculate the standard errors of the estimates (i.e., the parameter covariance matrix), you may get infinite, NaN, or absurdly large values. Larch also may emit a warning here, to alert you to a possible overspecification problem.

m2.calculate_parameter_covariance()
m2.parameter_summary()

/tmp/ipykernel_7252/1346125230.py:1: PossibleOverspecification: Model is possibly over-specified (hessian is nearly singular).
  m2.calculate_parameter_covariance()

	Value	Std Err	t Stat	Signif	Null Value	Constrained
Parameter
Cost	-0.0200	0.00	NA		0.00	fixed value
Income_Bus	0.0284	NA	NA		0.00
Income_Car	0.0478	NA	NA		0.00
Income_Walk	0.00	NA	NA		0.00
Mu_Motorized	1.00	0.00	NA		1.00	Mu_Motorized ≤ 1.0
Time	-0.0100	0.00	NA		0.00	fixed value

If you get such a warning, you can check the model’s possible_overspecification attribute, which may give you a hint of the problem. Here we see that the three Income parameters are highlighted in red.

m2.possible_overspecification

	(1) 0.0001057
Income_Bus	0.577350
Income_Car	0.577350
Income_Walk	0.577350

Reporting

Larch includes a variety of pre-packaged and a la carte reporting options.

Commonly used report tables are available directly in a Jupyter notebook through a selection of reporting functions.

m.parameter_summary()

	Value	Std Err	t Stat	Signif	Null Value	Constrained
Parameter
Cost	-0.0200	0.00	NA		0.00	fixed value
Income_Bus	0.0284	0.0353	0.81		0.00
Income_Car	0.0478	0.0386	1.24		0.00
Mu_Motorized	1.00	0.00	NA		1.00	Mu_Motorized ≤ 1.0
Time	-0.0100	0.00	NA		0.00	fixed value

m.estimation_statistics()

Statistic	Aggregate	Per Case
Number of Cases	4
Log Likelihood at Convergence	-3.82	-0.95
Log Likelihood at Null Parameters	-4.04	-1.01
Rho Squared w.r.t. Null Parameters	0.055

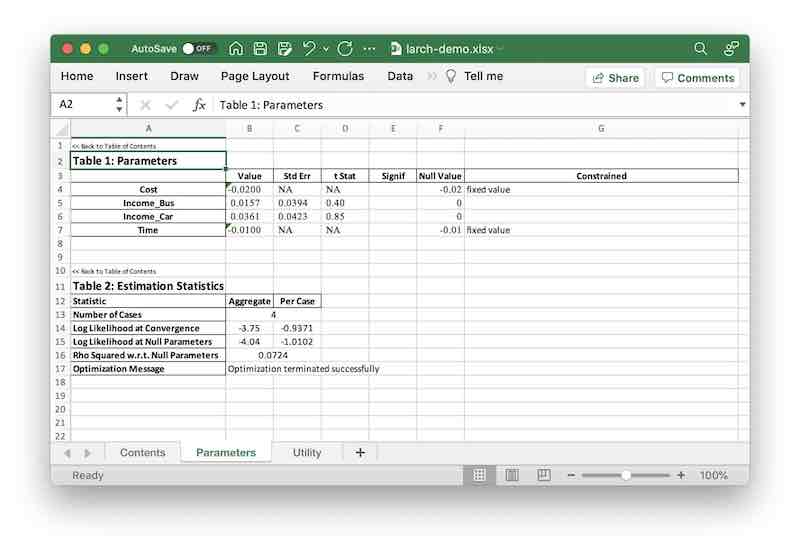
To save a model report to an Excel file, use the to_xlsx method.

m.to_xlsx("/tmp/larch-demo.xlsx")